مریم میرزاخانی و، شهود هندسی قوی
آهنگ آغاز و پایان ویدئو، لاکامپانِلا La Campanella (زنگ کوچک)، از «نیکولو پاگانینی» است. این نام را «فرانتس لیست» به موومان سوم از ویولن کنسرتوی شمارهٔ ۲ پاگانینی، داد. وجه تسمیهٔ آن این است که صدای یک زنگ کوچک در سراسر قطعه به گوش می‌رسد و با ویولن همراهی می‌کند.
وقتی این یاداشت را تنظیم می‌کردم مریم میرزاخانی به میهمانی خاک نرفته بود.
آنچه او هم نوست و هم کهن است
سخن است و در این سخن سخن است
یادگاری کز آدمیزاد است
سخن است آن دگر همه باد است
آید آواز هر کس از دهلیز
روزی آواز ما برآید نیز
چون من این قصه چند کس گفتند
هم در آن قصه عاقبت خفتند
چند باشی نظامیا در بند
خیز و آوازه‌ای برآر بلند
با آرزوی بهبودی مریم میرزاخانی ریاضیدان فرهیخته و با وقار ایرانی اشاره کوتاهی به زندگی او می‌کنم. مریم حدود دو سال پیش از انقلاب، پا به عرصه هستی گذاشت. درآغاز می‌خواست نویسنده شود اما ذوق و شوق ریاضی و زیبایی‌های آن وی را به عالمی دیگر کشید. خودش گفته‌است: برای من مسایلی وجود دارد که بیشتر از ۱۰سال است که روی آنها کار می‌کنم، با وجود این هنوز نتیجه‌ای نگرفته‌ام اما ناامید نمی‌شوم. بدون علاقه‌داشتن به ریاضی شما ممکن است آن را سرد و بیهوده بیابید. اما زیبایی ریاضیات خود را به شاگردان صبور نشان می‌دهد.
او توانست یک سری رشته‌های ریاضی را با ارتباط‌های غیر منتظره، بهم پیوند دهد و با این کار، متد تازه‌ای در حل مسائل ریاضی ابداع کند که تا آنزمان استفاده نشده بود. دوباره به این موضوع برمی‌گردیم.
مریم میرزاخانی در دوران تحصیل در دبیرستان فرزانگان تهران، برنده مدال طلای المپیاد جهانی ریاضی در سال‌های ۱۹۹۴ (هنگ‌کنگ) و ۱۹۹۵ (کانادا) شد و در این سال به عنوان نخستین دانش‌آموز ایرانی جایزه نمرهٔ کامل(۴۲ از ۴۲ را) گرفت. وی نخستین دختری بود که به تیم المپیاد ریاضی ایران راه یافت، نخستین دختری بود که در المپیاد ریاضی ایران طلا گرفت، نخستین کسی بود که دو سال مدال طلا گرفت و نخستین فردی بود که در آزمون المپیاد ریاضی جهان هم نمرهٔ کامل گرفت. از همان سال‌های دبیرستان موضوعاتی چون Graph «گراف»(مدل ریاضی برای یک مجموعه گسسته که اعضای آن به طریقی به هم مرتبط هستند) و Apollonius' theorem مسائل آپولونیوس(تعدادی مسئله در هندسه اقلیدسی که در آنها نحوه رسم یک دایره با سه ویژگی خاص، مورد پرسش قرار گرفته‌است)، مشغله ذهنی مریم میرزاخانی بود.
وی سال ۱۹۹۹ کارشناسی خود را در رشته ریاضی از دانشگاه شریف و سال ۲۰۰۴ دکترای خود را از دانشگاه هاروارد گرفت و به استادی دانشگاه استنفورد رسید. وی پس از عضویت در دو آکادمی ملی علوم فرانسه و مجمع فیلسوفان آمریکا، نهایتاً به آکادمی ملی علوم آمریکا پیوست(سال ۲۰۱۶).
ادوارد فرنکل Edward Frenkel، نویسنده کتاب «عشق و ریاضی» Love and Math، مریم میرزاخانی را «ریاضیدانی بزرگ و انسانی فوق‌العاده» خوانده و با اشاره به پیشتازی او به عنوان یک ریاضیدان زن، گفته‌است که کارهای وی الهامبخش زنان و مردان بسیاری خواهد بود.
...پروفسور مریم میرزاخانی با ورود به دانشگاه هاروارد به سطوح هذلولی علاقمند شد، این سطوح آمیب‌گونه(با مسامحه آمیب Amoeba، چون آمیب شکل خاصی ندارد)، این «فُرم»های آمیبی شکل، یا بهتر بگویم دوناتی شکل(دونات= شیرنی‌های گرد)، دارای دو یا چند سوراخ هستند که از یک هندسه غیراستاندارد برخوردارند و به طور کلی، به هر نقطه روی سطح، یک شکل زین‌مانند می‌دهند. دونات‌های هذلولی را نمی‌توان در فضای عادی ساخت چرا که در حس انتزاعی وجود دارند و فواصل و زوایا بر اساس مجموعه خاصی از معادلات محاسبه می‌شوند.
هر دونات Doughnut به روش‌های نامتناهی می‌تواند از یک ساختار هذلولی برخوردار شود....
ریاضیدانان سالیان دراز به دنبال یافتن راه حل عملی برای محاسبه حجم رمزهای جایگزین فرم‌های هندسی هذلولی بودند. ذکر و فکر مریم نیز محاسبه حجم رمزهای جایگزین فرم‌های هندسی هذلولی بود. سال ۱۳۷۸، با محاسبه‌ی عمق حلقه‌های ترسیم‌شده روی سطوح هذلولی، راهی عملی و کاربردی برای حساب کردن حجم فرم‌های هندسی هذلولی، ارائه داد. پیش از تلاش وی، برخی از سؤالات ساده در مورد سطوح هذلولی هنوز بی‌جواب مانده بودند. یکی از آنها در مورد ژئودزیک‌ها یا خطوط راست در سطح هذلولی بود.
...
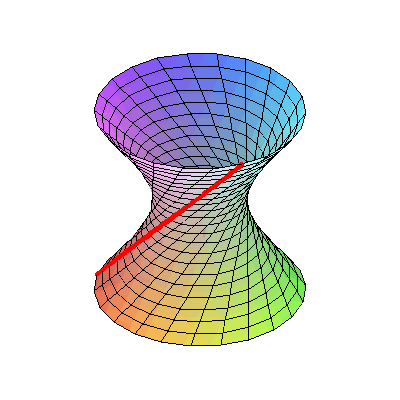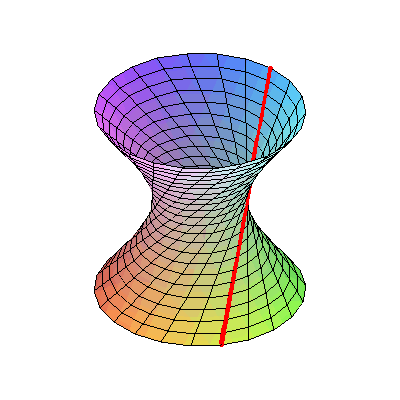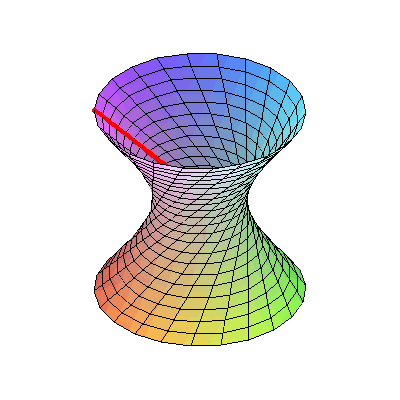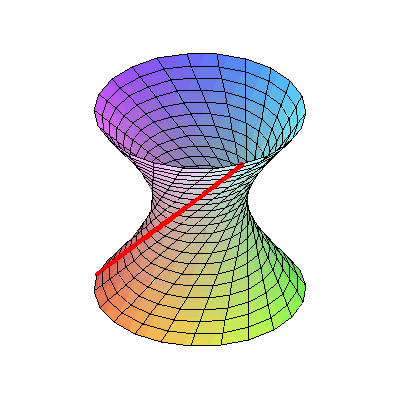
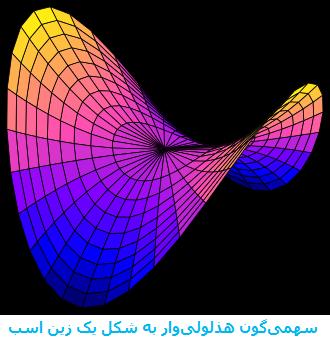مریم مطالعه سطوح هذلولی را با استفاده از فضاهای پیمانه‌ای متمرکز در دستور کار قرار داد و با محاسبهٔ عمق حلقه‌های ترسیم شده بر روی سطوح مورد بحث، آن را حل کرد. وی با اشاره به اینکه حتی یک سطح منحنی می‌تواند دارای یک مفهوم پاره خط مستقیم باشد که کوتاه‌ترین خط بین دو نقطه است، یادآور شد در یک سطح هذلولی، برخی ژئودزیک‌ها(خطوط راست) دارای طول بی‌نهایت هستند اما برخی دیگر در یک حلقه بسته می‌شوند. فضای هذلولوی، در مقابل فضای اقلیدسی قرار دارد که معتقد است تنها و تنها یک خط موازی با یک خط مشخص می‌تواند از یک نقطه‌ی ثابت عبور کند.
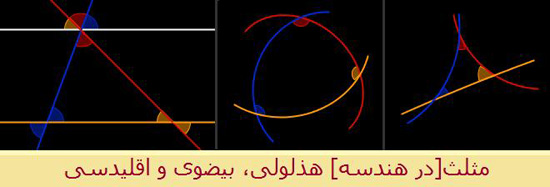
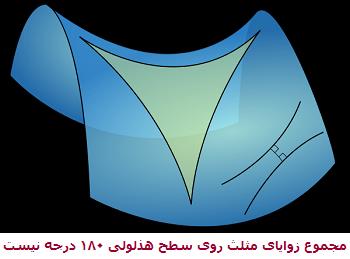در فضای هذلولی غیر اقلیدسی، تعداد بی‌شماری از خطوط موازی می‌توانند از یک نقطه ثابت عبور کند و مجموع زاویه‌های یک مثلث هم ۱۸۰ درجه نیست. در چنین فضای منحنی، کوتاه‌ترین مسیر بین دونقطه به‌عنوان ژئودزیک شناخته می‌شود. تحقیقات مریم میرزاخانی شامل محاسبه انواع خاصی از ژئودزیک(ژئودزیک بسته‌ی ساده روی سطوح هذلولوی) بود....
در سال ۲۰۱۴ مریم میرزاخانی به خاطر کار بر «دینامیک و هندسه سطوح ریمانی و فضاهای پیمانه‌ای آنها» مدال فیلدز Fields Medal را که از آن به نوبل ریاضیات تعبیر می‌شود به خود اختصاص داد. مدال فیلدز بالاترین جایزه در ریاضیات است و او نخستین زن و نخستین ایرانی برنده آن است.
وقتی این جایزه به مریم میرزاخانی تعلق گرفت، کمیته مدال فیلدز وی را این چنین توصیف کرد: «چیره‌دست در گستره قابل توجهی از تکنیک‌ها و حوزه‌های متفاوت ریاضی، او تجسم ترکیبی کمیاب است از توانایی تکنیکی، بلندپروازی جسورانه، بینش وسیع و کنجکاوی ژرف»
او که با سرطان دست و پنجه نرم می‌کرد، هنگام دریافت مدال فیلدز، تازه از شیمی‌درمانی فارغ شده بود. موهای کوتاهش(در آن موقع) نیز، همین را نشان می‌داد. مریم پیشتر موهای بلندی داشت.
تحقیقات مریم میرزاخانی در ریاضی به شاخه‌های مختلفی از جمله هندسه هذلولوی Hyperbolic geometry، هندسه جبری، توپولوژی، سیستم‌های دینامیکی و نظریه احتمال مرتبط بوده و آنها را به هم مرتبط و زمینه‌ساز روش‌های جدیدی در این شاخه‌ها شده، از جمله اینکه دیدگاه و اثبات بدیعی از برخی مسائل مطرح ریاضی، همچون حدس «ادوارد ویتن» در مورد فضای زمینه سطوح ریمانی، یا شار «ویلیام ترستن» در سیستم‌های دینامیکی به دست می‌دهند. نظریه‌ی شار زلزله «ویلیام ترستن» برای مدت‌ها به‌عنوان مسئله‌ای بی‌پاسخ در ریاضی شناخته می‌شد و مریم در سال ۱۳۸۹، آن را روی فضای تایشمولر Teichmüller space به اثبات رساند.
(شار Flux = میزان جریانی است که از واحد سطح در واحد زمان می‌گذرد
سال ۱۳۹۳، مریم میرزاخانی بهمراه دو محقق دیگر، ثابت کرد که ژئودزیک‌های مختلط و بستارهای آنها، برخلاف آنچه گفته می‌شود، به طرز شگفت‌انگیزی منظم‌‌اند...
...
جدیدترین کار مریم میرزاخانی و همکارانش اثبات حدسی در حوزه فضاهای زمینه مختلط است که علیرغم تلاش ریاضیدانان برای مدت‌ها حل‌نشده باقی مانده بود. وی در شمار محققانی بود که در حوزه‌های گوناگونی از گرافیک رایانه‌ای تا ریاضیات و علوم رباتیک، افق‌های تازه‌ای در مرزهای جهان اطراف ما گشوده‌اند.
مطالعات مریم میرزاخانی در زمینه نظریه توابع، ستایش بسیاری از ریاضیدانان را برانگیخته بود. گفته می‌شود او بدون گرفتن جایزه فیلدز هم در میان معروف‌ترین ریاضیدانان جهان بوده‌است.
...
تا کنون در مقالات و متون علمی مختلف نزدیک به ۱۰۰۰ بار به مطالعات مریم میرزاخانی ارجاع داده شده‌است. در مورد یکی از کارهایش «هندسه مسیر بی‌نهایتِ توپ بیلیارد» که با یکی از همکارانش «الکس اسکین» Alex Eskin به سرانجام رسانده، گفته شده، ممکن است به یکی از تئوری‌های مهم ریاضی منجر شود.
موضوع انتخابی مریم و اسکین استاد دانشگاه شیکاگو، کار روی رفتارهای توپ بیلیارد هنگام حرکت روی میز و برخوردش به لبه‌های میز بیلیارد بود. یک چالش ریاضی که فیزیکدانها به مدت یک قرن با آن دست و پنجه نرم می‌کردند. این تحقیق(تعیین مسیر یک توپ بیلیارد در یک میز چندضلعی که به نظر ساده می‌آید)، به مقاله‌ای ۲۰۰ صفحه‌ای منجر شد که وقتی در سال ۲۰۱۳ انتشار یافت، از آن با عنوان «آغاز عصری جدید» در ریاضیات یاد شد. مساله بیلیارد می‌تواند مثال ساده‌ای از یک سیستم دینامیک باشد که در آن سیستم در طول زمان، براساس مجموعه‌ای از قواعد، تکامل می‌یابد و از طرف دیگر پیش‌بینی مسیر حرکت توپ به‌طور عجیبی غیرقابل محاسبه باقی می‌ماند...
پانویس
نشریه پاپیولار ساینس در آمریکا که هرساله ده دانشمند برگزیدهٔ را معرفی می‌کند، سال ۲۰۰۵، مریم میرزاخانی را ازجمله به این دلیل که در حوزه‌های گوناگونی از گرافیک رایانه‌ای تا ریاضیات و علوم ربوتیک، افق‌های تازه‌ای در مرزهای جهان اطراف ما گشوده‌است، به عنوان یکی از ۱۰ ذهنِ برتر در رشتهٔ ریاضیات برگزید و به او لقب صف شکن Dambuster داد. وی به جز جایزه فیلد، جوایز دیگری هم گرفته‌است. ازجمله، جایزه بلومنتال در سال ۲۰۰۹، جایزه ستر Satter Prize از انجمن ریاضی آمریکا در سال ۲۰۱۳ (Ruth Lyttle Satter Prize in Mathematics)
...
پایان‌نامه پروفسور میرزاخانی(شمردن خم‌های بسته بر رویه‌های دارای ساختار هذلولوی)، شامل سه مقاله بود که در سه مجله عالی ریاضیات یعنی Annals of Mathematics، Inventiones Mathematicae و مجله انجمن ریاضی آمریکا منتشر شد. این در حالی است که عموم ریاضیدانان در طول عمر کاری‌شان موفق به چاپ حتی یک مقاله هم در این سه ژورنال نمی‌شوند. موضوع پایان‌نامه وی به بررسی چگونگی محاسبه حجم‌های ویل-پیترسونی فضاهای مدول هم مرز سطوح ریمان، پرداخته که شامل شمارش حلقه‌های در سطوح دارای هندسه هذلولی است.
زمینهٔ تحقیقاتی مریم میرزاخانی مشتمل بر فضاهای تایشمولر Teichmüller space، هندسه هذلولَوی(هندسه هایپربولیک یکی از هندسه‌های نااقلیدسی که به هندسه لباچفسکی نیز مشهور است)، نظریه ارگودیک(شاخه‌ای از علم ریاضیات که سیستم‌های پویا با یک معیار ثابت و مسائل مربوط به آنها را بررسی می‌کند)، «فضاهای مدولی»( فضای تمام ساختارهای هذلولوی بر یک رویه)، و هندسه هم‌تافته است. استادانش گفته‌اند کار او از ماهیتی عمیقاً نظری برخوردار بود ولی در عین حال می‌توانست بر فیزیک نظری و نحوه به وجود آمدن کیهان تأثیر بگذارد و از آن‌جا که کارش به نظریه میدان‌های کوانتومی هم مربوط می‌شد، می‌توانست کاربردهایی در مهندسی و علوم مواد داشته باشد. ضمن اینکه در داخلِ ریاضیات نیز نتایجی برای مطالعه اعداد اول و رمزنگاری در بر داشت.
کارهای ریاضی پروفسور مریم میرزاخانی با معرفی ایده‌هایی جدید و پیوند‌دادن شاخه‌های مختلفی از ریاضیات، پیشرفت‌های بسیار مهمی را در مطالعه رویه‌های ریمان و خانوادۀ آنها رقم زده‌است. شاخه‌هایی نظیر هندسه هذلولوی، آنالیز مختلط، توپولوژی، سیستم‌های دینامیکی و هندسۀ جبری شمارشی در کارهای وی به هم پیوند می‌خورند.
رسالۀ دکترای پروفسور مریم میرزاخانی با موضوع «شمردن خم‌های بسته بر رویه‌های دارای ساختار هذلولوی»، در کنار نتایج مهم و ارزندۀ دیگر و نوآوری‌های فراوان، اثباتی جدید از حدس ادوارد ویتن Edward Witten ـ که ماکسیم کنتسویچ Maxim Kontsevich به خاطر اولین اثبات از آن در سال ١٩٩٨ جایزه فیلدز را دریافت کرد در خود داشت. این رساله خیلی زود مورد توجه تعداد زیادی از ریاضیدانان قرار گرفت. مریم میرزاخانی معتقد بود که جهان از قوانین هندسه‌ی هذلولی پیروی می‌کند؛ به همین علت برای محاسبه‌ی اشکالی که فرم هندسی مرتبی ندارند، می‌توان با رسم حلقه‌هایی روی سطوح آنها، حجم دقیق آنها را حساب کرد. این روش، اثبات جدیدی برای تئوری‌های ادوارد ویتن و ماکسیم کنتسویچ در مورد تعداد نقاط متقاطع سطوح پیمانه‌ای در فضاهای هندسی هذلولی به شمار می‌آمد.
...
رویه‌های ریمان، با مسامحه، سطوحی شبیه رویه تایر خودرو است. با دو حفره یا بیشتر، که به‌واسطه هندسه غیرمتعارف‌شان که به هندسه ریمانی مشهور است، هر نقطه‌ای از آنها شکلی زین‌مانند دارد.
Mirzakhani, M. (July 2010). "Ergodic Theory of the Earthquake Flow". International Mathematics Research Notices.
سنایی، احسان - یک ذهن زیبا: مریم میرزاخانی
مریم میرزاخانی، رؤیا بهشتی زواره، کتاب نظریهٔ اعداد، Elementary Number Theory, Challenging Problems
همه نوشته‌ها و ویدئوها در آدرس زیر است:
...
همنشین بهار
برای ارسال این مطلب به فیس‌بوک، آیکون زیر را کلیک کنید:
facebook